汉诺塔一文速通

汉诺塔一文速通

问题背景

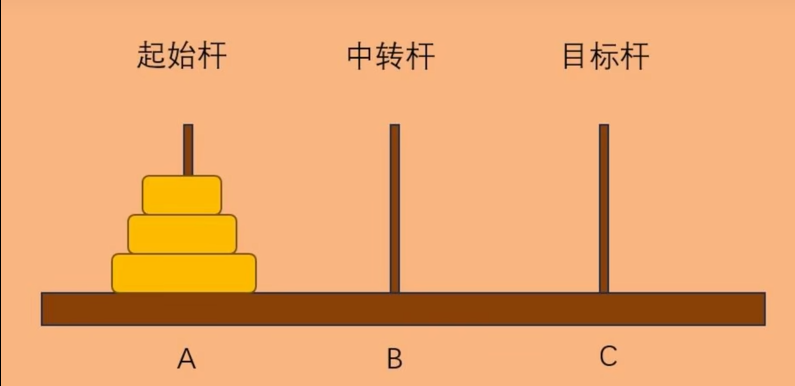
  • 有三根柱子，通常标记为 A（起始杆）、B（中转杆）、C（目标杆）。
  • 开始时，所有的圆盘都按照从大到小的顺序堆叠在一根柱子（假设为 A 柱）上。
  • 目标是将所有圆盘从起始柱子（A 柱）移动到目标柱子（比如 C 柱）。
  • 移动过程中有两个重要的规则：每次只能移动一个圆盘；在移动过程中，大圆盘不能放在小圆盘上面。

image-20241201102242192

本质分析

实际上，以三个汉诺塔为例，我们需要把最上面两个盘借助C转移到B上，（此时C是中转杆，B是目标杆），再直接将最大的底盘移动到C（目标杆），最后借助A，将B上的n-1个盘转移到C上（此时B是起始杆，A为中转杆，C为目标杆）。

当汉诺塔的盘数增加，其底层逻辑都不变，依旧是：

  • 将除底盘外的n-1个底盘移动借助目标杆到中转杆上
  • 直接将最大底盘移动到目标杆上
  • 将中转杆上的n-1个盘借助起始杆移动到目标杆上。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include <stdio.h>
void print(char x,char y)    //移动函数，负责输出移动步骤
{
    printf("%c -> %c\n",x,y);
}
void hanoi(int n, char start,char temp,char end)//第一位是起始，第二位中转，第三位目标
{
    if (n==1)              //如果只有一个盘，可以直接移动
    {
        print(start,end);  
    }
    else {
        hanoi(n - 1,start,end,temp);  //将非底盘（n-1）个从起始柱借助目标柱移动到中转柱
        print(start,end);             //将底盘从起始站柱子移动到目标柱
        hanoi(n - 1,temp,start,end);  //将非底盘（n-1）从中转柱子借助起始柱移动到目标柱子
    }
}
int main()
{
    int n;
    scanf("%d",&n);
    hanoi(n,'A','B','C');   //这里默认设定A为起始柱，B为中转柱，C为目标柱。
    return 0;
}