数据结构8：图

图

基本概念

图是由顶点的有穷非空集合和顶点之间边的集合组成的。
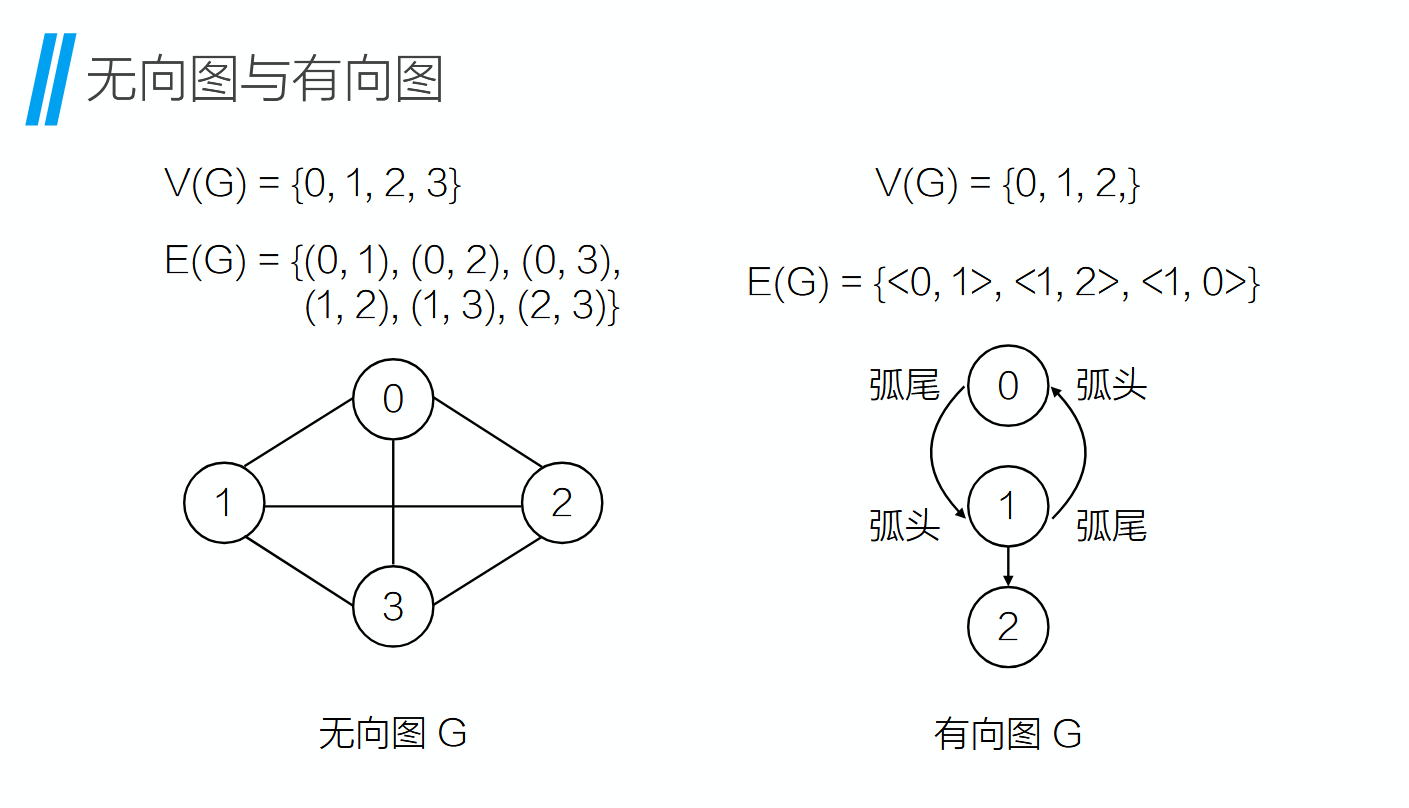
通记为 G(V, E)，其中 G 表示一个图，V 是图 G 中顶点的集合，E 是边的集合
V(G) 和 E(G) 通常分别表示图 G 的顶点集合和边集合。

对于图这种数据结构，不允许没有顶点，但边集可以为空。（点可以是孤立的）

image-20250526200457954

简单图与多重图

1.图中不能有指向自身的环

2.同一条边在图中不能出现两次或以上

不满足以上两条限制的图称为多重图

完全图

完全图：具有最多边数的图
对于一个具有 n 个顶点的无向完全图，边数量的最大值为 n(n - 1) / 2
对于一个具有 n 个顶点的有向完全图，边数量的最大值为 n(n - 1)

路径和路径长度
路径：从一个顶点开始，经过一系列的边到达另外一个顶点形成的顶点序列。
路径长度：路径上边的条数
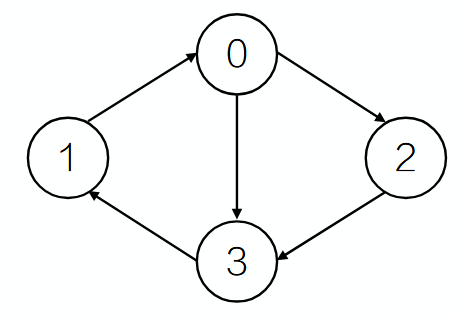
回路（环）：起点和终点相同，路径 {0, 3, 1, 0} 是一个回路（环）

简单路径
简单路径：如果路径中不出现相同的顶点，则称为简单路径

简单回路：除第一个顶点和最后一个顶点外，其余顶点不重复出现的回路称为简单回路

顶点的度

度：对于无向图，顶点的度指的是与顶点相关联边的数目。
入度：在有向图中，对于顶点 v，箭头指向 v 的边的数目。
出度：在有向图中，对于顶点 v，从该顶点出发的边的数目。

度和边的关系

在无向图中，假设具有 n 个顶点，e 条边
图中所有顶点度之和等于边数的两倍
对于有向图，所有顶点的出度之和与入度之和相等，弧的数量也相等。

子图

就是类似于子集之类的一个定义

连通图
连通：在无向图中，如果从顶点 V 到顶点 w 有路径，则称顶点 v 到顶点 w 是连通的。
如果对于图中任意两个顶点都是连通的，则称此图为连通图

连通分量
无向图中的极大连通子图称为连通分量
连通分量为子图
子图为连通图
连通子图含有极大顶点数
具有极大顶点数的连通子图包含依附于这些顶点的所有边。

强连通图
强连通图：在有向图中，对于每一对顶点 v 和 w ，从 v 到 w 和从 w 到 v 都有路径，
则称该有向图是强连通图。
有向图中的极大强连通子图称为有向图的强连通分量。

生成树
生成树：指含有图中全部顶点的极小连通子树（连通图的极小连通子图）
注意：包含所有顶点 n，但只有足以构成一棵树的 n-1 条边

边的权和网
在一个图中，每条边可以标注上一个代表某种含义的数值，该数值称为这个边的权值
网：边上带的权值的图，也称为带权图

图的存储结构

邻接矩阵

邻接矩阵（Adjacency Matrix）是图（Graph）的一种存储结构，通过二维数组表示顶点之间的连接关系。其核心原理是将图的顶点和边信息分别用一维数组和二维矩阵存储，适用于描述图的拓扑结构，尤其适合稠密图（边数接近顶点数平方）。

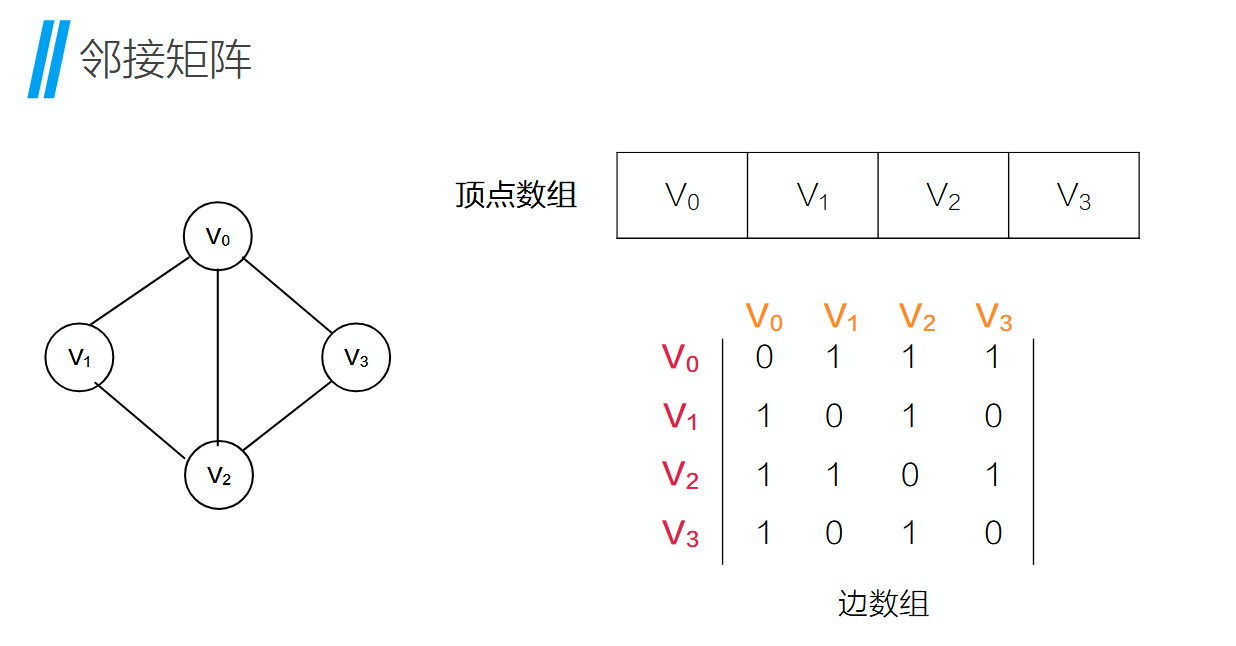
image-20250527103145031

如果有连线在矩阵中就是1表示，如果没有就是0表示

无向图中一般是关于对角线对称的

有向图中的矩阵就不是这样

但是如果是带权值的图

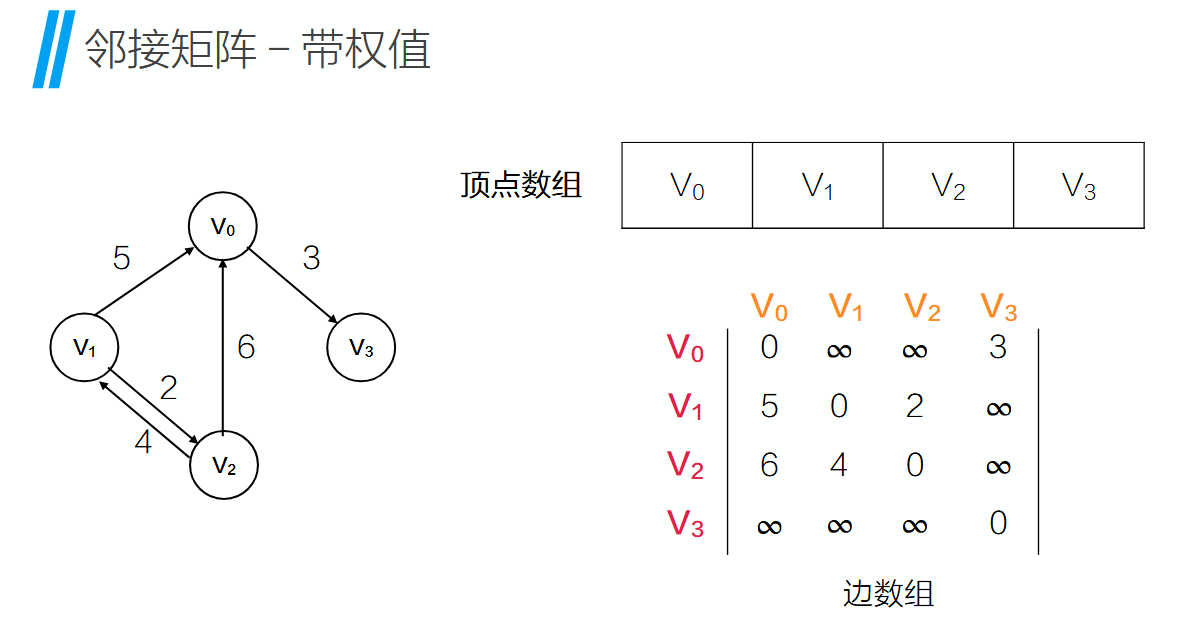
image-20250527110250144

两个边之间没有关系在矩阵中表示为0。

邻接表

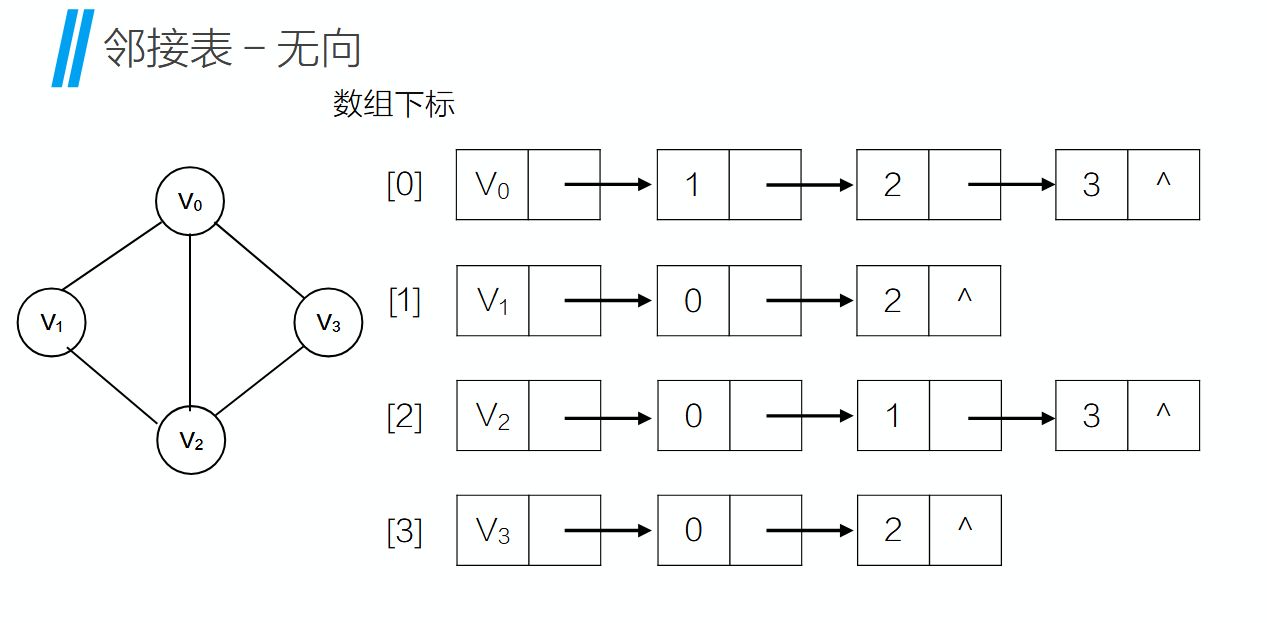
邻接表（Adjacency List）是图（Graph）的一种链式存储结构，结合了顺序存储和链式存储的特点，能够高效表示稀疏图并支持动态操作。

图中构成了四条链表，而链表的头节点就是各个顶点，这四个链表都存放在一维数组中，而第二个元素开始的数据域就是一维数组的元素的索引，所以我们可以使用这种路径来实现图的遍历。

有时候基于顶点的边不是固定顺序的，比如，下图中V0有指向V1，V2和V3的三条边，那么第一条链表中的第二第三第四元素可以自由交换位置。

image-20250527111402078

在有向图中，根据方向我们可以有逆邻接表

逆邻接表

它和邻接表相反，头节点是终点，后面的元素是起点。

十字链表

十字链表（Orthogonal List）是一种专为有向图设计的链式存储结构。

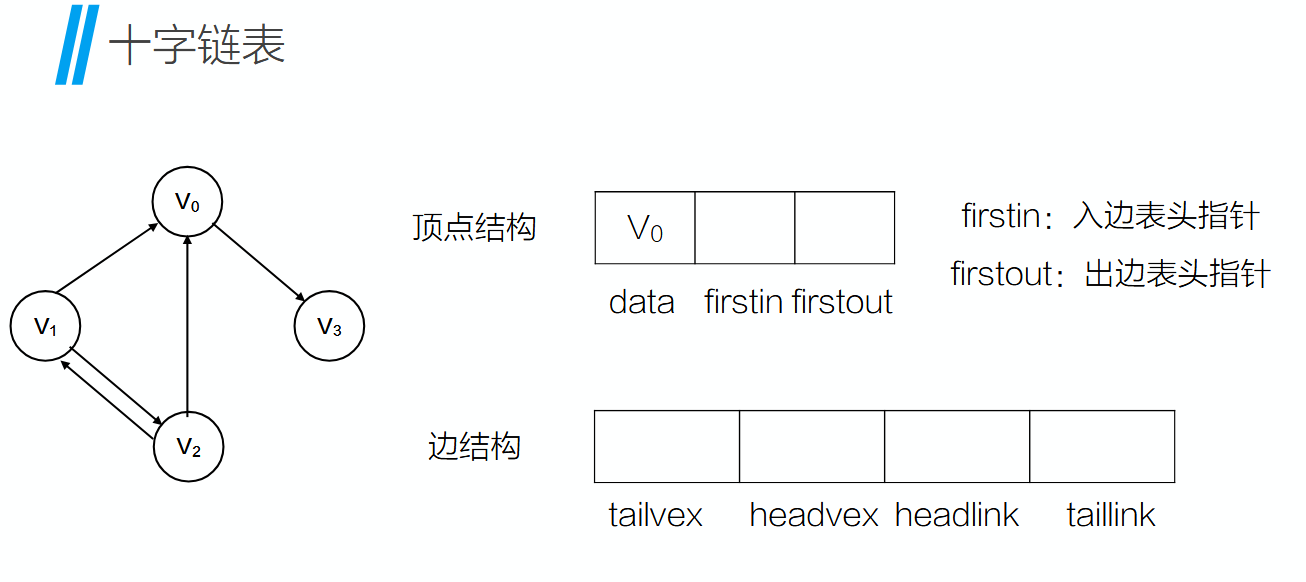
十字链表有两个结构：顶点结构和边结构

入边就是“进入该顶点的边\弧\箭头”，出边反之。

Vex指的是顶点，Tailvex表示弧尾，Headvex表示弧头，后面Headlink表示弧头的指针，taillink表示弧尾的指针

image-20250527133314864

下面我们讲解一个橙色箭头的意思，根据上文，顶点结构的第二个格子应该是入边的指针，所以我们需要找到”进入”该顶点的弧，并且让该顶点的第二个格子的指针指向它。

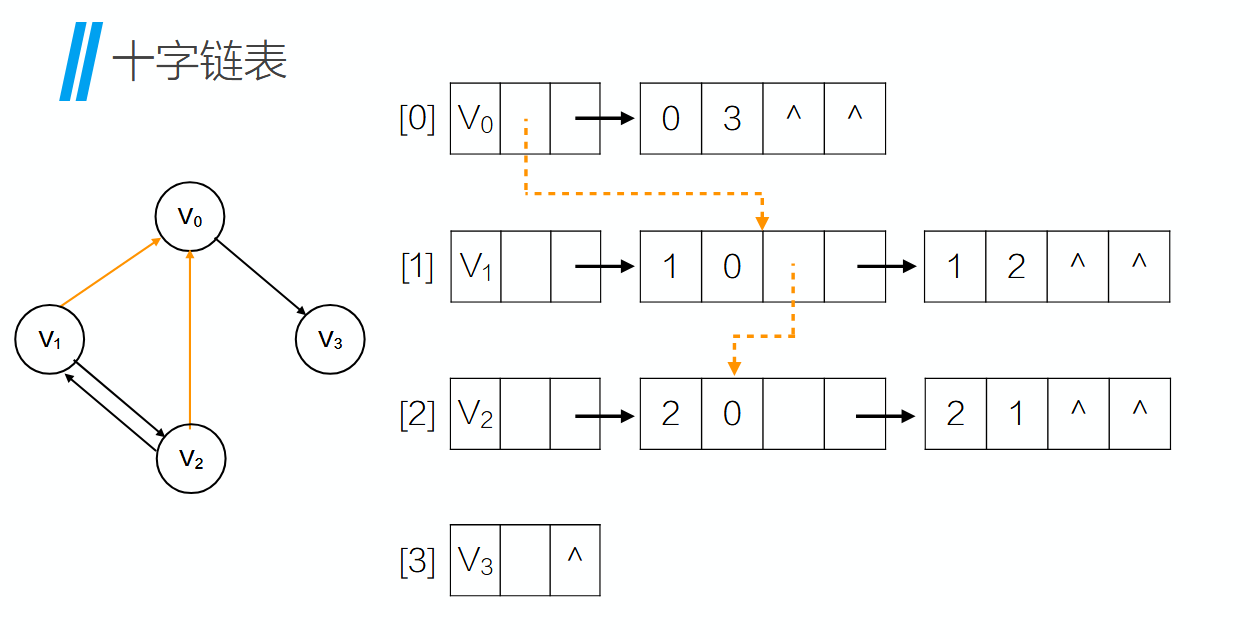
image-20250527190943882

用横向来表达出边的路径，用纵向来表达入边的路径，纵横交错形成了Crossing，也就是十字链表。

邻接多重表

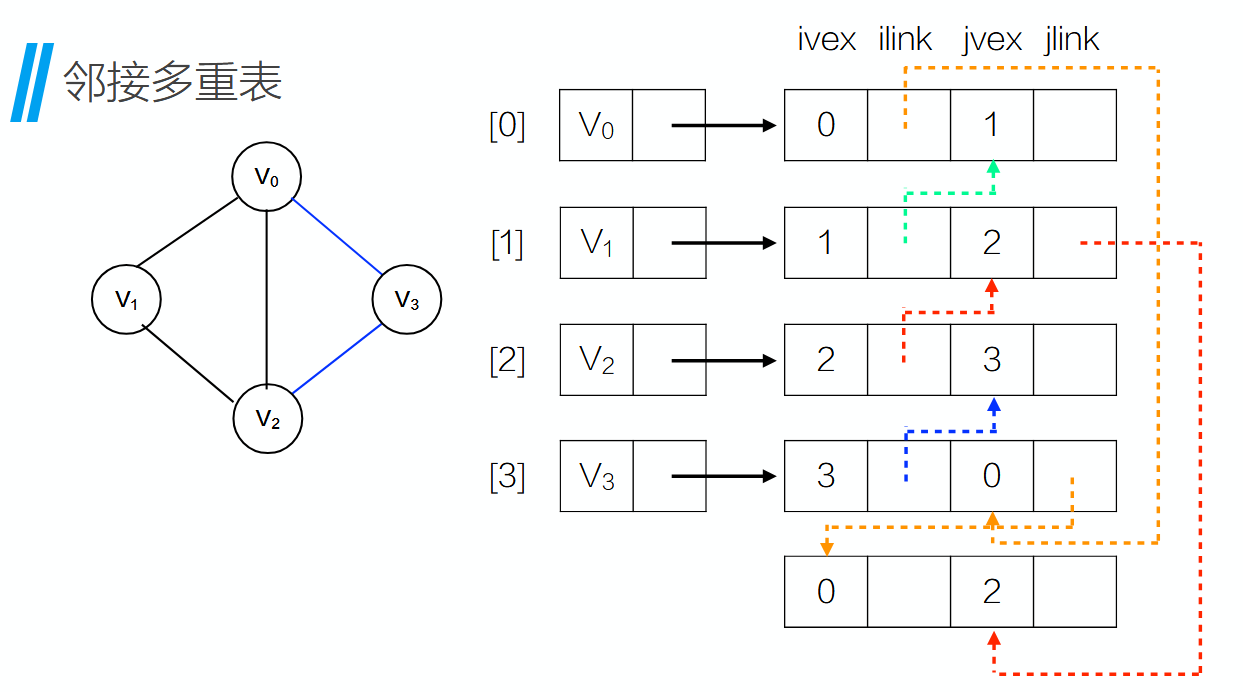
邻接多重表是专为无向图设计的一种链式存储结构，通过优化邻接表的冗余存储问题，显著提升了空间效率与边操作能力。以下从结构特性、应用场景及对比分析等角度进行详细介绍：

image-20250527193509055

将顶点连接到与他相关的边上，随即将link连接到未涉及的边上。

image-20250527195518243

写在最后

如果你看到这里，那么这段时间对数据结构的学习算是告一段落了。按之前的安排，这之后应该还要三个章节，分别是DFS和BFS，Dijkstra最短路径算法和拓扑排序，但是我打算将他放到算法的学习章节中去。

写下这段文字的时间是六月二号，按道理，我将提前两周开始复习大学的期末考试，祝看到这里的人好运，我们再会。