数据结构4：双向链表

数据结构4：双向链表

前情提要

上次我们讲到了局部有环的单链表。

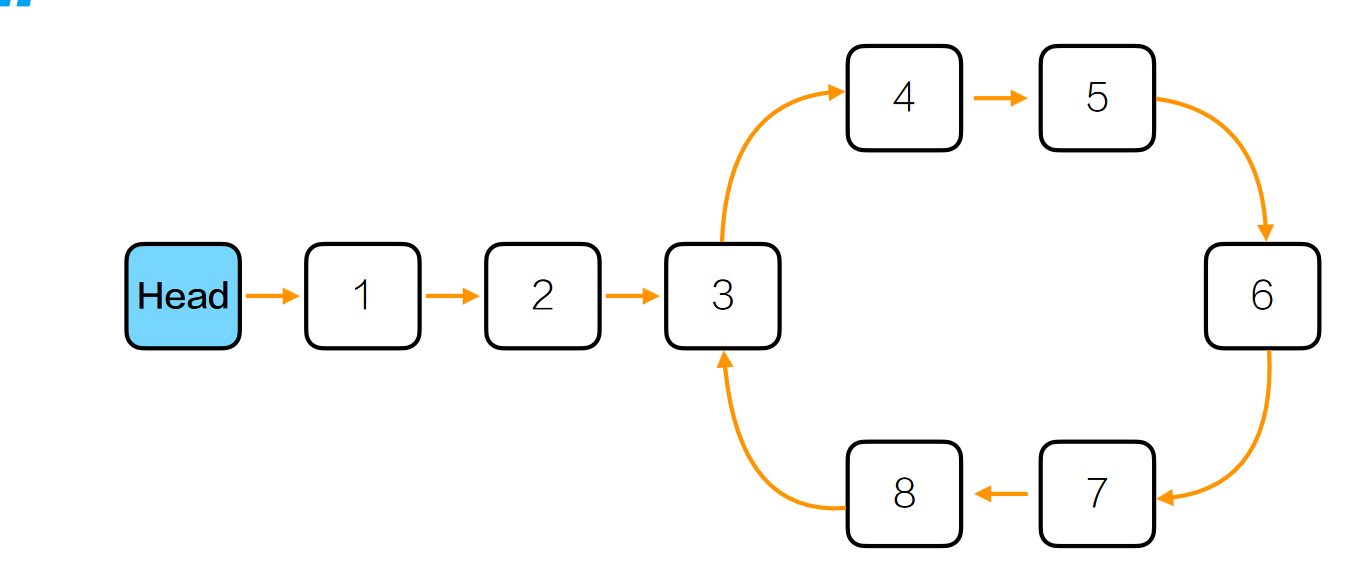
pE626V1.png

循环链表：找出入口和长度

现在需要你找出一个循环链表的环入口。

我们的步骤是：

  • 设定快指针的速度是慢指针的两倍。
  • 当快慢指针相遇时，慢指针已经走了 k 步，快指针走了 2k 步。
  • 当快慢指针相遇时，我们已经进到了环中
  • 现在设立一个新指针指向快指针，使其遍历并记录步数直到与快慢指针相遇，步数就是环长度。
  • 初始化快慢指针为头指针，然后让快指针前进【环长度】步
  • 让快慢指针以相同速度前进，直到相遇，相遇点就是入口

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
void findroundBegin (Node *head){
    Node *fast = head;
    Node *slow = head;
    while(fast->next!= NULL && fast->next->next != NULL){  //循环找到环的入口
        fast = fast->next->next;
        slow = slow->next;
        if(fast == slow){  //如果快指针和慢指针相遇，则说明有环
            Node *p = fast;
            int count = 0;
            while(p-> next != slow){
                count++;  //循环计数,表示环的长度
                p = p->next;
            }
            fast = head;
            slow = head;
            for(int i = 0; i < count; i++){  //循环找到环的入口
                fast = fast->next;
            }
            while(fast != slow){  //循环找到环的入口
                fast = fast->next;  //两者的速度同步
                slow = slow->next;
            }
            printf("环的入口为：%d\n", fast->data);
            return slow;
        }
    }

双向链表

链式存储结构的节点中只有一个指示直接后继的指针域，由此，从某个结点出发只能顺指针向后寻查其他节点。若要寻查结点的直接前驱、则必须从表头指针出发。换句话说，在单链表中，查找直接后继的执行时间为O(1)，而查找直接前驱的执行时间为O(n)。
为克服单链表这种单向性的缺点，可利用双向链表（Double Linked List)。在双向链表的节点中有两个指针域，一个指向直接后继，另一个指向直接前驱。

节点示例：

1
2
3
4
typedef struct  Node{
    int data;
    struct Node 8prev,*next;
}Node;

这就生成了一个节点，该节点有一个数据域和两个指针域。

头插法

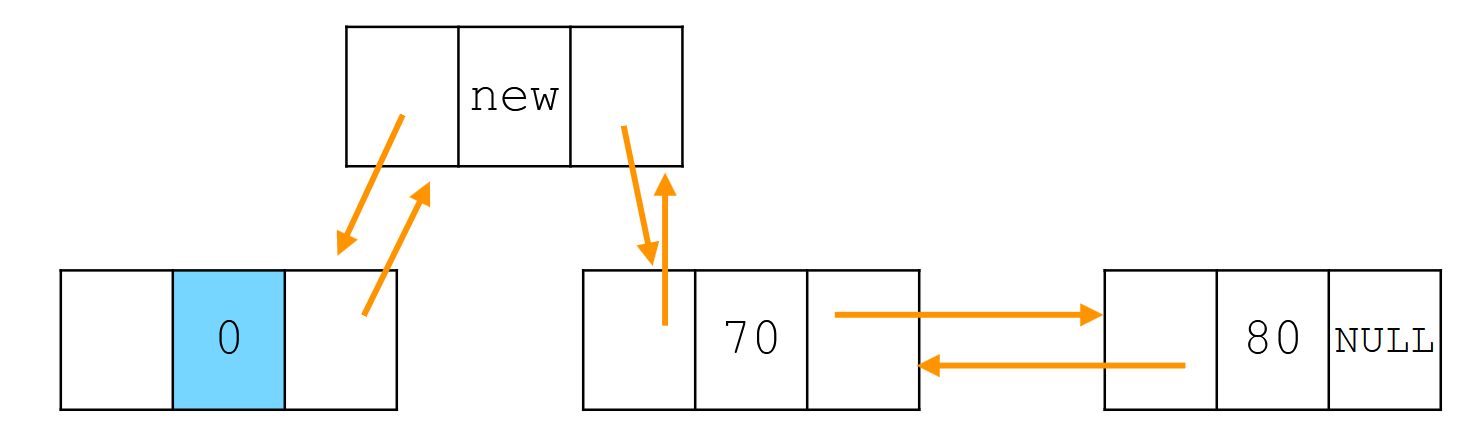
image-20250405145646106

类似地，插入一个新节点，我们的步骤如下：

  • 使得新节点的prev指针指向头指针，next指针指向头指针的后一个节点。
  • 使头节点的后一个节点的prev指针指向新节点
  • 使头节点的next指针指向新节点

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void insert_head(Node *head,int data)
{
    Node *new_node = (Node*)malloc(sizeof(Node));
    new_node->data = data;
    new_node->prev = head;
    new_node->next = head->next;
    if (head->next != NULL)
    {
        head->next->prev = new_node;
    }
    head->next = new_node;
    return 1;

}

尾插法

这个相对于头插法的步骤更简单，但是时间复杂度会比较高：

  • 找到尾节点，把尾节点的next指针指向新节点
  • 把新节点的prev指针指向尾节点，next指针指向Null

代码实现：

1
2
3
4
5
6
7
8
9
// 尾插法,传参直接传入尾节点。
Node* insertTail(Node *tail, ElemType e) {
    Node *p = (Node*)malloc(sizeof(Node));
    p->data = e;
    p->prev = tail;
    tail->next = p;
    p->next = NULL;
    return p;
}

指定位置插入节点

类似于单链表的插入，移动到指定点，然后插入。

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
void insertAtPosition(Node** head, int position, int value) {
    // 创建新节点
    Node* newNode = (Node*)malloc(sizeof(Node));
    newNode->data = value;
    newNode->prev = NULL;
    newNode->next = NULL;

    // 如果链表为空，直接设置为头节点
    if (*head == NULL) {
        *head = newNode;
        return;
    }

    // 如果插入位置为0，直接插入到头部
    if (position == 0) {
        newNode->next = *head;
        (*head)->prev = newNode;
        *head = newNode;
        return;
    }

    // 找到插入位置的前一个节点
    Node* current = *head;
    int count = 0;
    while (current != NULL && count < position - 1) {
        current = current->next;
        count++;
    }

    // 如果位置超出链表长度，返回错误
    if (current == NULL) {
        printf("插入位置超出链表长度\n");
        free(newNode);
        return;
    }

    // 插入新节点
    newNode->next = current->next;
    if (current->next != NULL) {
        current->next->prev = newNode;
    }
    current->next = newNode;
    newNode->prev = current;
}

双向链表和顺序表的对比

比较项目 存储结构 顺序表 链表
存储空间 预先分配，会出现闲置或溢出现象 动态分配，不会出现存储空间闲置或溢出现象
空间 存储密度 不用为表示节点间的逻辑关系而增加额外的存储，存储密度等于 1 需要借助指针来体现元素间的逻辑关系，存储密度小于 1
存取元素 随机存取，按位置访问元素的时间复杂度为 O(1) 顺序存取，按位置访问元素时间复杂度为 O(n)
时间 插入、删除 平均移动约表中一半元素，时间复杂度为 O(n) 不需要移动元素，确定插入、删除位置后，时间复杂度为 O(1)
适用情况 1) 表长变化不大，且能事先确定变化的范围2) 很少进行插入或删除操作，经常按元素位置序号访问数据元素 1) 长度变化较大2) 频繁进行插入或删除操作