第四章：数据的表示与运算

计算机的世界中，只有零和一两种表示。

将各种表示用0和1的二进制来表示的过程，就是编码。

广义上的定义是：

编码，就是用少量简单的基本符号对大量复杂多样的信息进行一定规则的组合

本章思维导图：

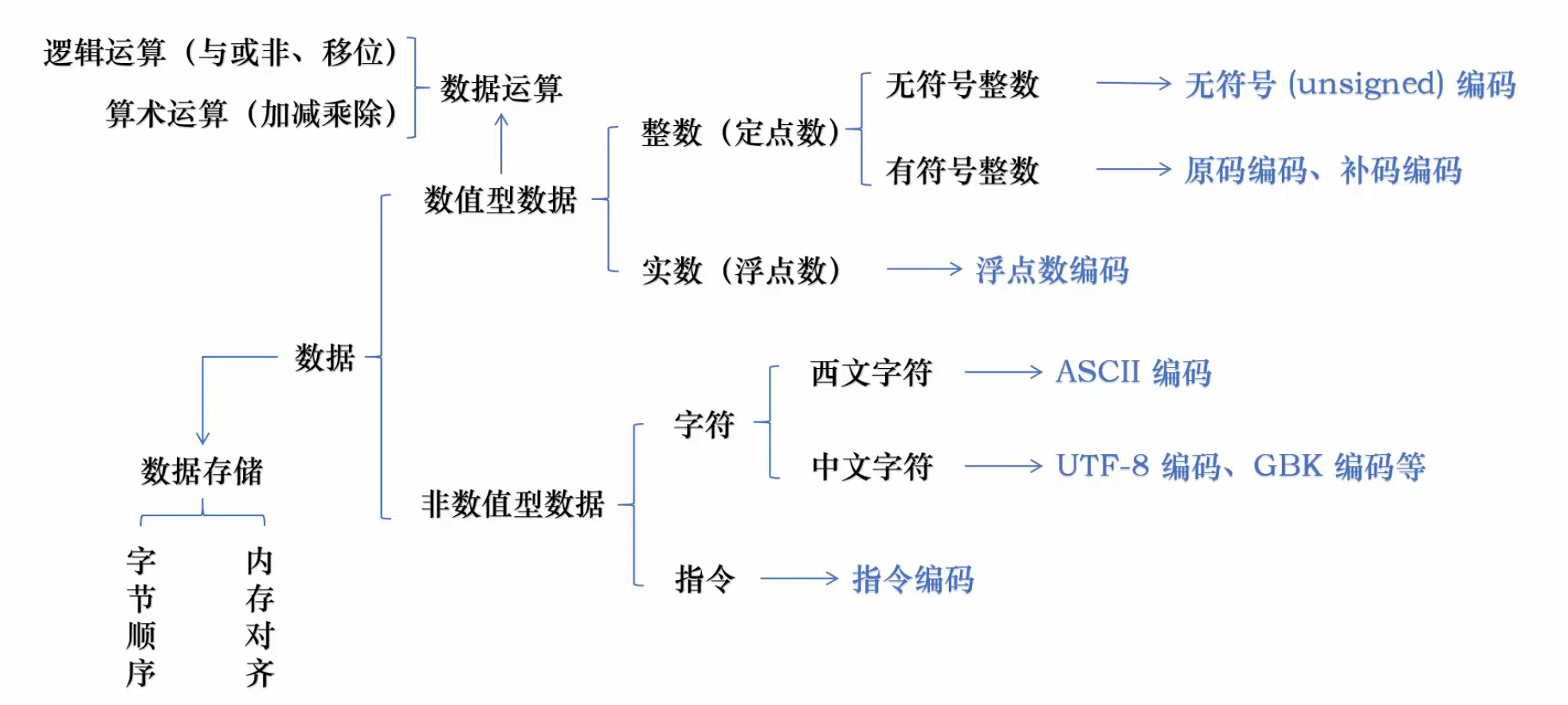
进制转换技巧

非数值数据的编码

无符号整数的编码

八个二进制位那么表示的无符号范围就是0-255，因为255对应的是八位全一，在加一就是256但是这种情况下发生了溢出，所以只能取到255

有符号整数的原码

第一位就是符号位，后面都是数值位

正数的原码反码补码都相同

负数的反码等于原码的符号位不变其余位取反，补码等于反码+1

补码（负数的补码）数值位取反+1就是原码

补码的存在有很强的进步性。

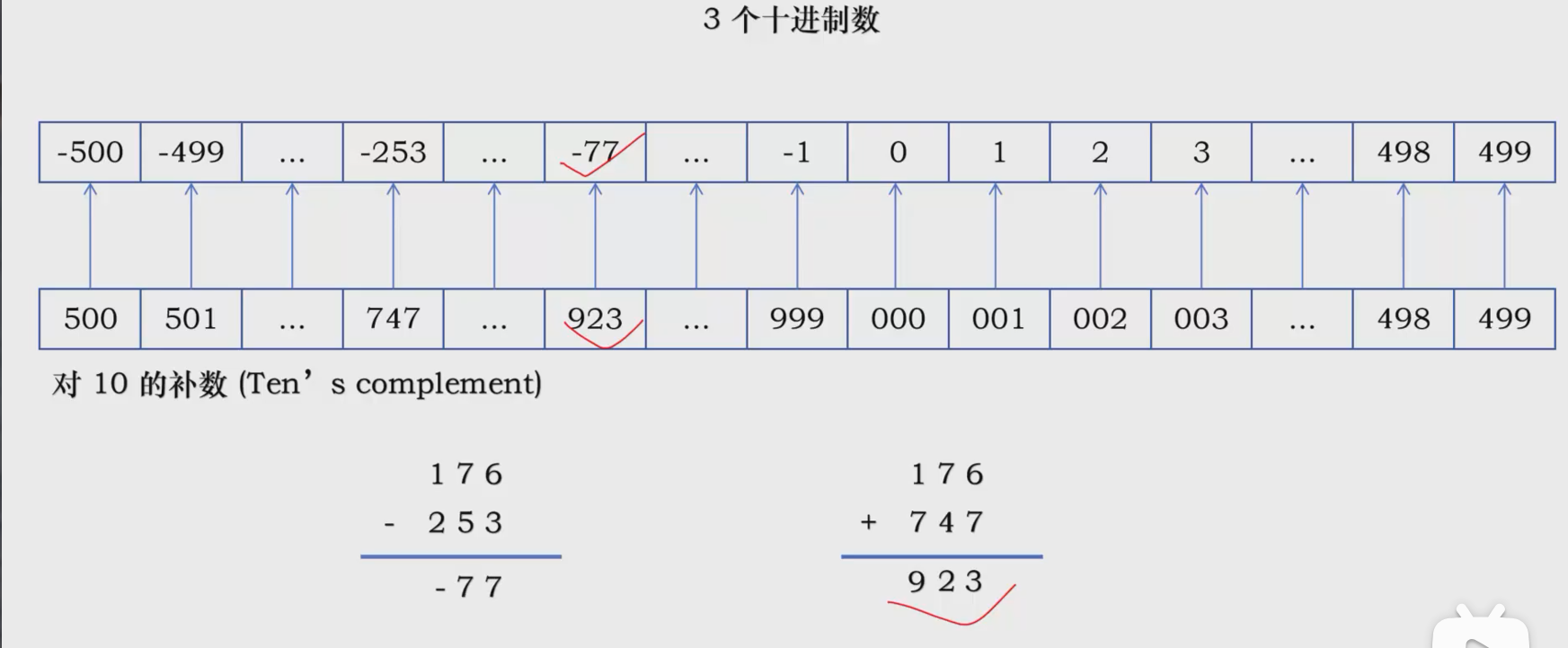
如果我们要使用无符号数表示符号数，对于0-499，我们可以直接表示，但是对于-500-0，我们的方法是求其补数（补数是一个在特定计数系统（模运算）下，能够“互补”使得结果达到某个“上限”的数。），也就是用500-999来表示，这么做很有利于计算。

比如，我们要计算176-253，那就是176+（-253），那–253对应747，那就是176+747就是923对应-77。我们也知道176-253就是-77，前后对得上，这就完成了计算。

补码中+0和-0是同一个表示

注意，如果说在二进制比较中1比0大，那么会出现****负数大于整数的情况

我们用移码来解决这个问题：

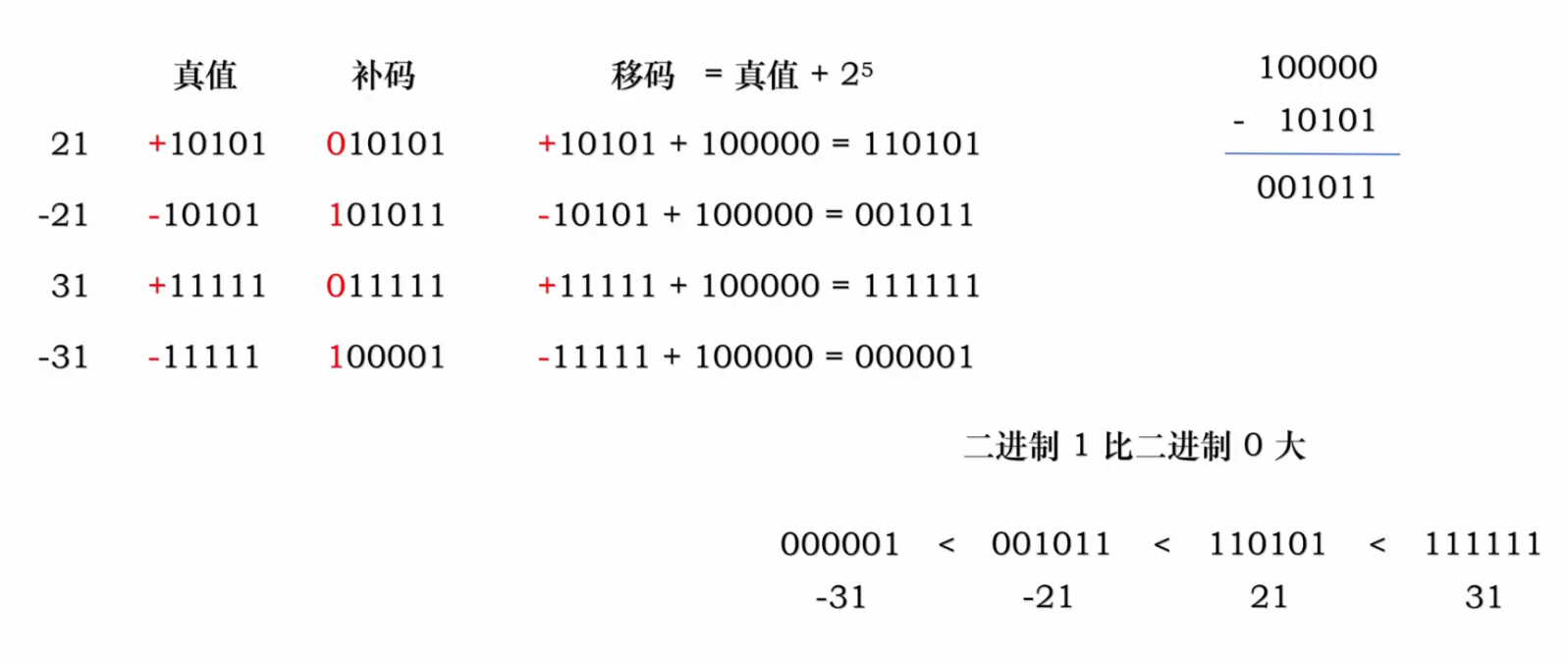
移码就是将数往某个方向移动一段距离从而统一符号。[X]移 = 2 ^ (n-1) + x，可表示的范围是-2^(n-1)到2^(n-1)-1,和补码的范围是一样的。

有符号数和无符号数的转换

无符号编码如果超过了正数范围转化后会变为负数。转换的C语音语句大概是

unsigned short uv =(unsigned short)v;

零扩展和位截断

如果将一个无符号数转换成一个更大的无符号类型的话，就需要执行零扩展（位扩展）。这就是扩大了数据的最大位数。

顺序是先进行零扩展在进行符号转换

反过来，如果需要将long转化为int或者short，就需要位截断

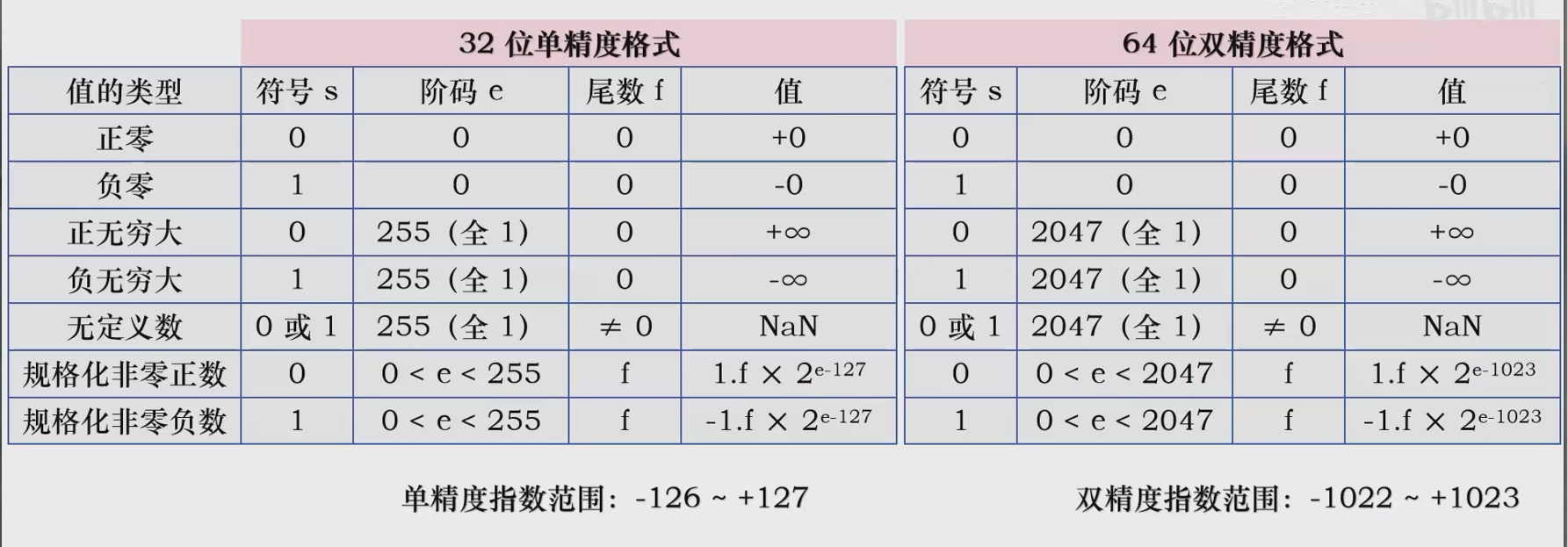
浮点数编码

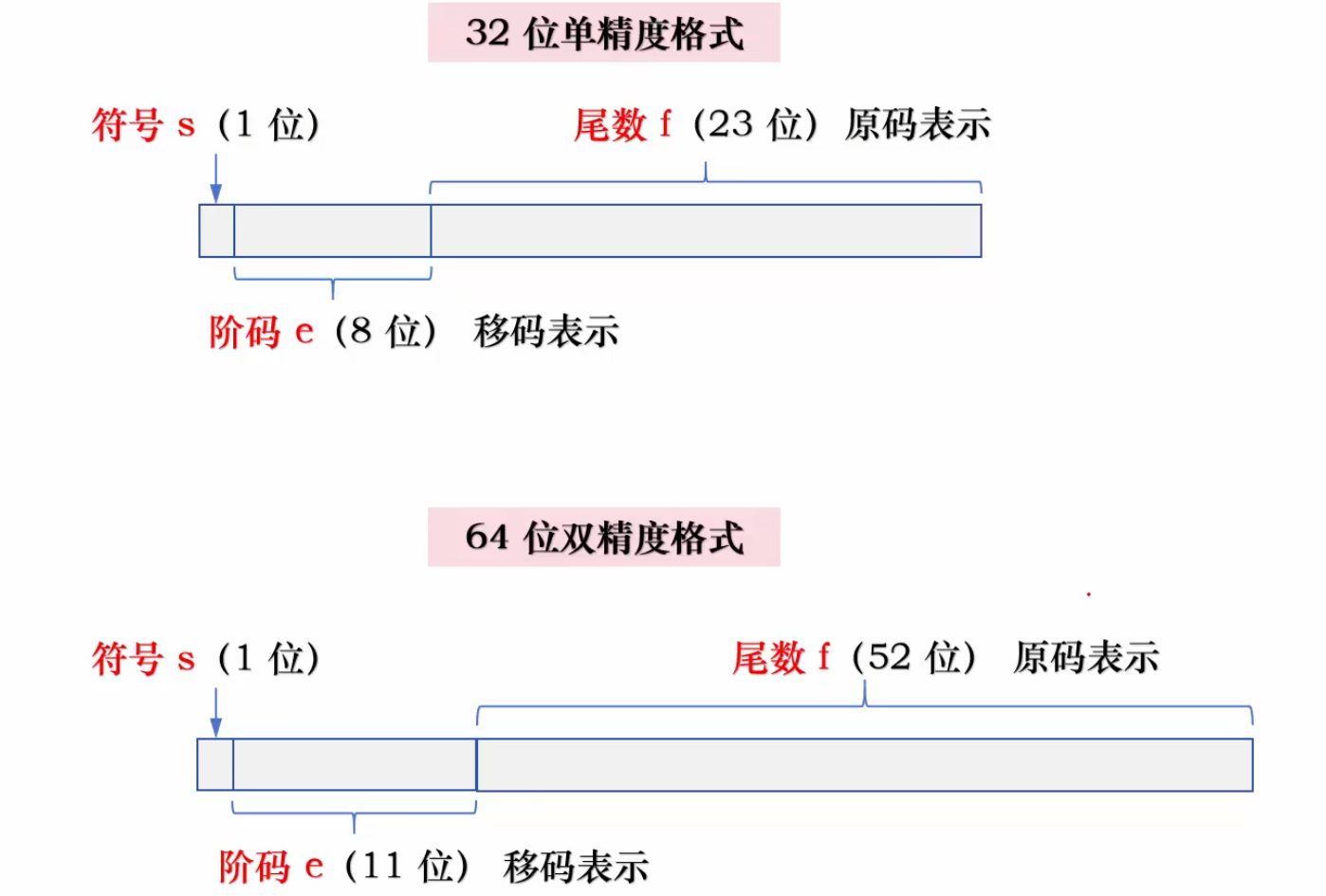
浮点数编码是使用科学计数法的方式来表示的，根据需要分为符号位S，指数域E（标定数的范围），尾数域M（决定数的精度）。

让我们以数字-12.375的单精度（32位）编码过程为例，来具体感受一下

处理符号：这是一个负数，所以**符号位 S设为 1**。

转换为二进制科学计数法： 先将 12.375转换为二进制。整数部分 12是 1100，小数部分 0.375是 0.011（因为 0.375=0.25+0.125=2−2+2−3）。 所以 12.375的二进制表示是 1100.011。

将其规格化：1100.011 = 1.100011 × 2^3。这里，**底数（尾数）是 1.100011，实际指数是 3**。

编码数：精度的偏移值是127。所以，存入指数域的值是 3 + 127 = 130。130的二进制是 10000010。所以**指数域 E为 10000010**。

编码尾数：从规格化后的尾数 1.100011中，取出小数部分 100011，然后在其右边补0，直到凑满23位。所以**尾数域 M为 100 0110 0000 0000 0000 0000**。

最终，-12.375的单精度浮点数编码结果就是将这三部分拼接起来：**1 10000010 10001100000000000000000**（为了方便阅读，这里用空格分开了符号位、指数域和尾数域）。

标准化的原因是尾数部分我们尽可能不让0占用精度，会移动小数点位置，位数部分往左移叫做左规，右移叫右规。

规格化浮点数的标志是尾数部分的最高位是1，但在IEEE 754标准中，这个1是隐含的。

IEEE 754浮点数规范

该规范解决了不同计算机数据不互通需要额外转化数据的问题。

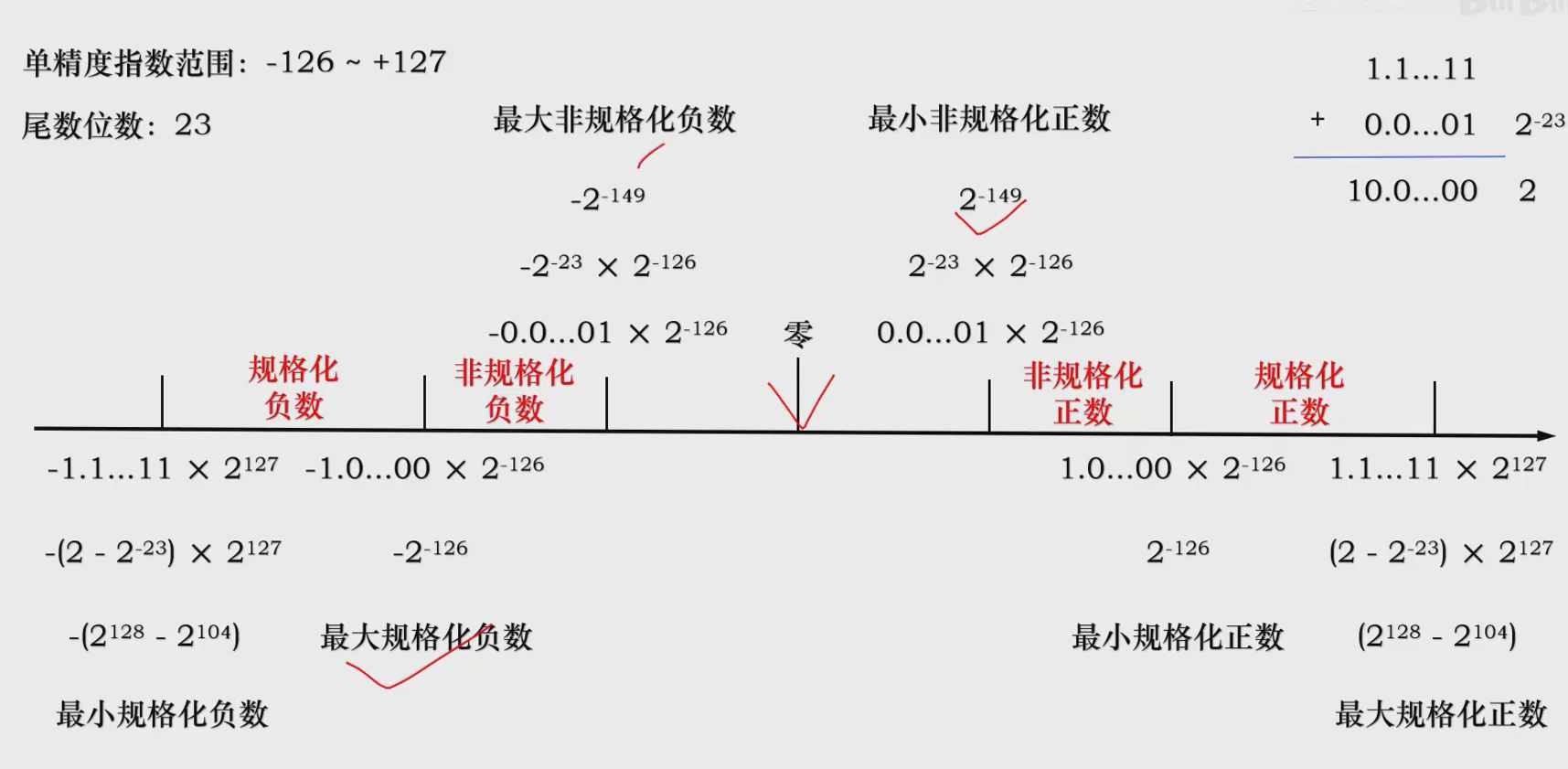
其他区间不能使用浮点数表示，属于溢出数，根据溢出的不同分为负上溢，负下溢，正上溢，正下溢。

数据一旦产生上溢，计算机必须中断运算操作，进行溢出处理。 而数据下溢时，浮点数值趋于零，计算机将其当作机器零处理。

非规格化数的特点：

• 阶码为0
• 尾数不为零
• 指数是-126
• 隐藏位是0，位数变化范围是0.0000····1 ~0.111····1

六十四位类似。